第三種電気主任技術者_平成22年度理論_問13

共振回路の等価抵抗に関する問題

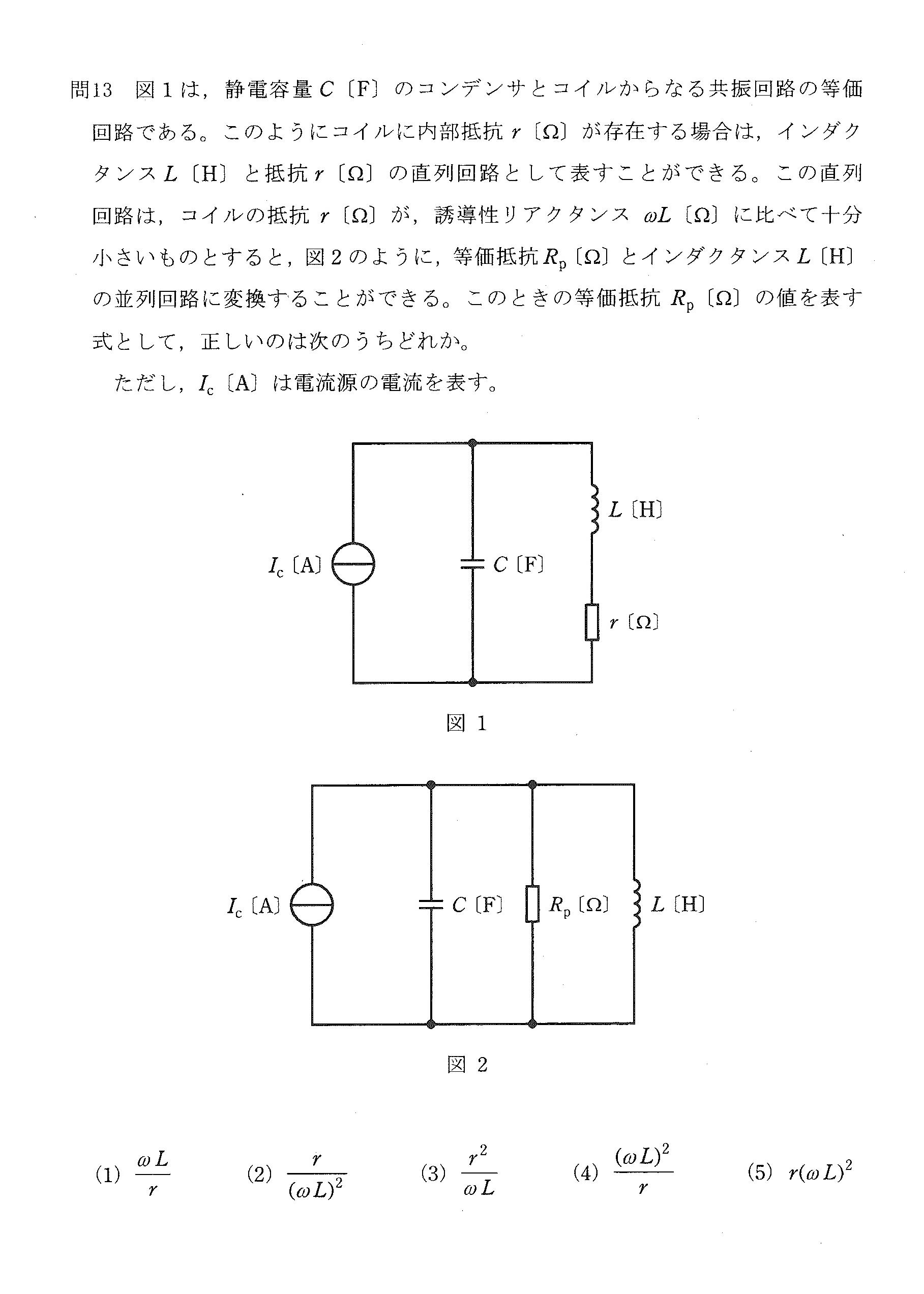
問題文(要約)

コイル(インダクタンス \( L \))と内部抵抗 \( r \) とが直列につながった回路を、抵抗成分が十分に小さい場合に並列回路に変換するとき、並列側の等価抵抗 \( R_p \) はどのように表されるかを問う問題です。選択肢は次の通りです。

1) \( \omega L / r \)
2) \( r / (\omega L)^2 \)
3) \( \frac{r^2}{\omega L} \)
4) \( \frac{(\omega L)^2}{r} \)
5) \( r(\omega L)^2 \)

重要度：必ず理解

RLC共振回路の等価変換や、コイルのQ（品質係数）の考え方につながる重要問題です。頻出テーマですので確実に押さえておきましょう。

出題意図とポイント

この問題では、コイルの直列抵抗 \( r \) が小さい場合、直列回路を並列回路に変換したときの並列等価抵抗 \( R_p \) を求める知識が問われます。
コイルのインダクタンス \( L \) に対するリアクタンスは \( \omega L \) となり、Q値の目安は
\[
Q = \frac{\text{インダクティブリアクタンス}}{\text{抵抗}} = \frac{\omega L}{r}
\]
となります。並列回路に換算すると、抵抗成分は \( Q^2 \) 倍になることがポイントです。

正答番号：4

解法の手順

STEP1. 基本の公式等を確認

まず、コイルのQ値は下式で定義されます。
\[
Q = \frac{\omega L}{r}
\]
並列回路側の抵抗 \( R_p \) は、Q値を用いると
\[
R_p = Q^2 \cdot r
\]
で表せることが知られています。これが直列回路と並列回路の等価変換時の基本的な考え方です。

STEP2. 数値を代入して計算

上記の式を用いると、
\[
R_p = \left(\frac{\omega L}{r}\right)^2 \times r
= \frac{(\omega L)^2}{r}
\]

STEP3. 答えを導く

よって、並列側の等価抵抗は
\[
R_p = \frac{(\omega L)^2}{r}
\]
となります。選択肢では (4) に該当します。

まとめ

今回の学習ポイントのまとめ

• コイルの直列抵抗 \( r \) が十分小さいとき、並列回路に換算すると抵抗成分は \( Q^2 \) 倍になる。
• Q値は \( Q = \frac{\omega L}{r} \) であり、よって並列回路側の等価抵抗 \( R_p \) は \( \frac{(\omega L)^2}{r} \) となる。
• RLC回路の共振や等価変換問題は、Q値の考え方と抵抗成分の置き換えが本質的なポイント。